Re-creating imaginary numbers in real life

From first principles thinking, the contemporary definition $i^2=-1$ is basically the same as $i=\sqrt{-1}$ despite the symbolic difference. Although the former feels less intimidating, both come to the same result $i^2=-1$ . The property $i^2=-1$ is used to define $i$ while $i$ itself is also used to define the property. Therefore, $i$ itself is still undefined, or is not based on a first principle or a thing that is already known. A first principle is a fundamental assumption that cannot be further deduced. Ancient Greek philosopher Aristotle (384 - 322 BCE) expressed a first principle as "the first basis from which a thing is known." It is no wonder many people are unsatisfied with $i=\sqrt{-1}$ that originates from nowhere in the real world (the unknown).

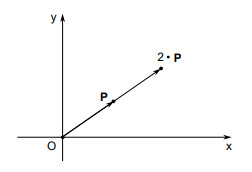
Vectors are directional entities with both magnitude (length) and direction, and they are ubiquitous in real life, appearing in physical quantities such as position, velocity, acceleration, and force. Real numbers can stretch vectors through multiplication. For example, the vector P is stretched by number 2 along a straight line and becomes the vector 2P.

By analogy, rotational numbers are introduced to rotate vectors through multiplication as well. A rotational number of angle θ, denoted [θ], rotates a vector counterclockwise by angle θ, relative to the vector’s initial direction with the vector’s magnitude unchanged.

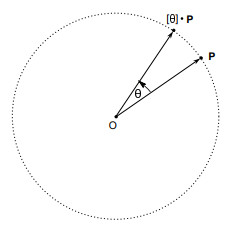
As illustrated, the vector P is rotated by rotational number [θ] and becomes the vector [θ]P.

As a result, the re-creation of the imaginary unit, complex numbers and Euler's formula as well as the discovery of a rotational number set can then be achieved without using and relying on $\sqrt{-1}$ or $i^2=-1$ . Like the real number set $\mathbb{R}$, a rotational number set $\mathbb{E}$ also exists in Nature. Members of $\mathbb{E}$ are in the radian range between $-\pi$ and $\pi$, covering all angles in 360 degrees. It is believed that if advanced aliens exist, they also have a similar concept about the existence of the real and rotational number sets, although their mathematics may take radically different forms from ours.

Similar to 0, 1 and −1 as special members in $\mathbb{R}$, there are also special members in $\mathbb{E}$, such as [0] of angle 0, [180] of angle 180 degrees, and [90] that is an orthogonal rotational number of angle 90 degrees. Let's examine the property of [90].

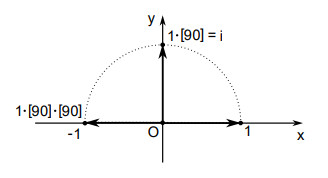
In the x-y plane, number 1 represents a point in the x-axis, and has an implied direction from the origin to the point, the same direction as that of the positive x-axis. Therefore, number 1 can be treated as a unit vector for the x-axis, and rotated by rotational numbers. Multiplying [90] to number 1 rotates the unit vector counterclockwise by 90 degrees with 1[90] pointing to the positive y-axis direction. Further multiplying [90] rotates the implied direction of 1[90] to the negative x-axis direction or the direction represented by –1. The process is expressed as 1[90][90] = −1. Let the orthogonal rotational number be designated by the symbol $i$ :

It then follows that $1·i·i=-1$ or $i^2=-1$. It is noted that in practice, the directions of the unit vectors 1 and $i$ are implied without being denoted by arrow. But, in our mind, we can still consider them as the unit vectors for the respective x- and y-axes.

As shown above, the orthogonal rotational number [90] in the set $\mathbb{E}$ happens to have the unique property $i^2=-1$ . By the same token, the number 1 (denoted $I$) in the set $\mathbb{R}$ happens to have the unique property $I^2=1$ . This also finally reveals imaginary numbers in our daily life through vector rotation.

The most important practical implication, particularly for learners, is that the complex plane is no longer needed and can be replaced by the familiar x-y plane, which has a direct connection to the real world.

For comprehensive development and extension, refer to the book Discovering Imaginary Numbers in Everyday Life: The Popularization of Complex Numbers.